

But you could always turn that into the form #y=mx+b# to find your slope #m# by simply solving for #y#. Parallel lines can be recognised by their equations by checking if their gradients are the same. Here, you can't directly pick out the slope. Check it out: Let's find the equation of the line that passes through the point. The problems in this section (and the next) are cool because they pull together a bunch of stuff I've shown you. Sometimes though, linear equations aren't in the form #y=mx+b#. So, two lines are parallel if they have the same slope. Line A y 2x 3 Line B 2y x + 3 Line C 4y 3x 2 Line D 2y 4x 1 Line E 3y 2x 2 Two of these lines are parallel. Note that they have to be different, because if they were equal, then you'd just have two identical lines that technically intersect in every single point. 10 Here are the equations of five straight lines. The parallel line needs to have the same slope of 2. The following video shows how write the equation of a line given a point on the line and a line that is parallel to it. In the general equation of a line #y=mx+b#, the #m# represents your slope value.Īn example of paralell lines would therefore be: Find the equation of the line that is: parallel to y 2x + 1 and passes though the point (5,4) The slope of y2x+1 is: 2. On the other hand, the slope of perpendicular lines are the negative reciprocals of each other, and a pair of these lines intersects at 90 degrees. So, to find an equation of a line that is parallel to another, you have to make sure both equations have the same slope. Lines that are parallel, in the sense of Euclidean geometry (geometry of the plane) are lines in the same plane that never intersect. Parallel lines continue, literally, forever without touching (assuming that these lines are on the same plane). Question 135170: How do I find the equation of a line parallel/perpendicular without a point that it goes through example: 圓x+9 (I dont have a point that it. Because of this, a pair of parallel lines have to have the same slope, but different intercepts (if they had the same intercepts, they would be identical lines).
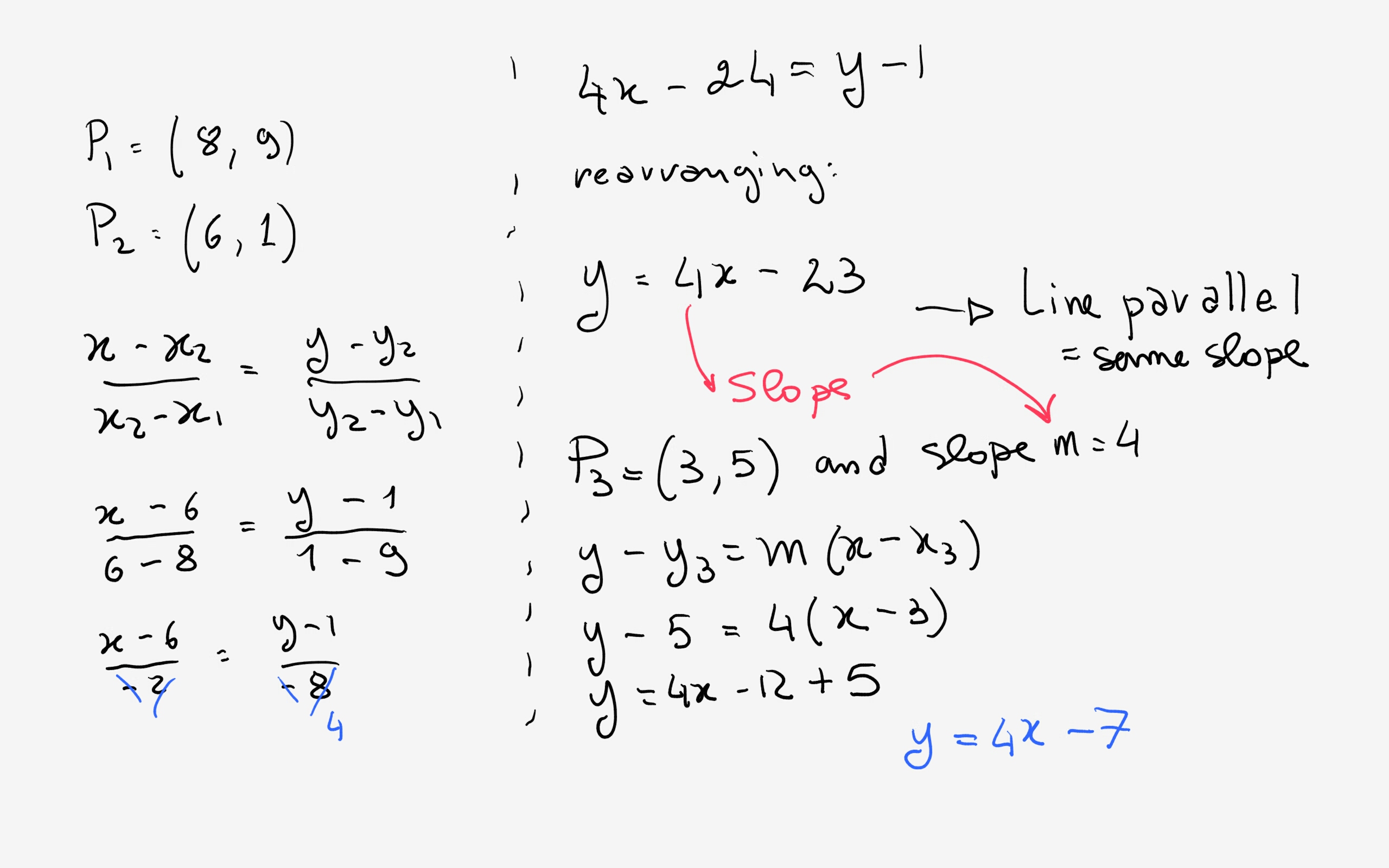
Perpendicular to \(x+7=0\) and passing through \((5, −10)\).Parallel lines are lines that never intersect.Solution : In the equation of the second line 10x + 14y + 5 0, the coefficients of x and y have the common divisor 2. Problem 5 : Verify, whether the following equations of two lines are parallel. Let c 1 be the y-intercept of the required line. So, the equations of the given two lines are parallel. Since the required line is parallel to the given line, the slope of the required line is also m. Proof : Let m be the slope of the line ax + by + c 0, Then, m - a b. Perpendicular to \(y−3=0\) and passing through \((−6, 12)\). The equation of the line parallel to a given line ax + by + c 0 is.


 0 kommentar(er)
0 kommentar(er)
